A New Method for Estimating Heating System Parameters: My Breakthrough – The Physical-Neural Network Model
A New Method for Estimating Heating System Parameters: My Breakthrough – The Physical-Neural Network Model
The principle of backpropagation has played a crucial role in the development and success of artificial neural networks training by fitting their inner parameters to a given dataset. But what if we use this principle for estimating other systems’ parameters? This was the idea of my postdoctoral research that was published recently. It uses the principle of backpropagation to estimate the parameters of a physical model for indoors electric heating and heat dissipation to forecast electricity demand. These parameters are crucial for understanding how heating systems consume energy and respond to external factors, like outdoor temperature and control actions. In this blog post, I will explain the method I’ve developed, which combines differential equations and neural networks to accurately estimate these parameters.
The Challenge
The challenge I faced was finding a way to accurately estimate the parameters of heating systems. These parameters govern the behavior of heating systems, and without precise knowledge of them, it’s challenging to optimize their performance. To address this challenge, I developed a parameter fitting algorithm aimed at finding the best parameter values to match the heating system’s energy consumption curve.
The Method
Let me break down the key steps of the method I developed:
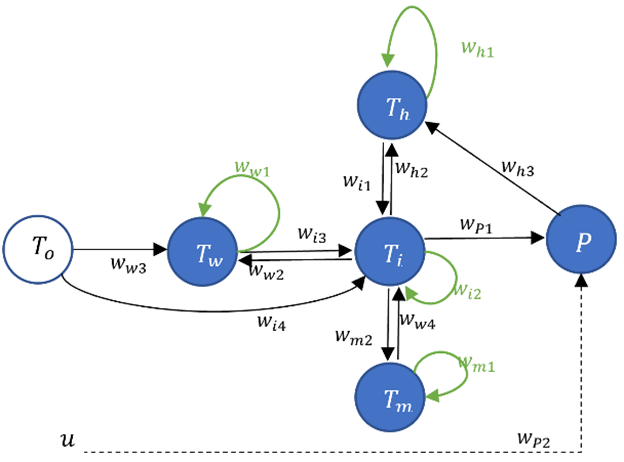
- Solving Differential Equations: The first step involved solving a set of differential equations in discrete time. For example, applying the Euler method to these equations yielded new values for various temperatures and heating power.
- Matrix Form: I transformed the equations into a matrix form for ease of computation. This transformation resulted in a set of equations that related the temperatures (T_h, T_i, T_w, T_m) and heating power (P) at different time steps.
- Weight Matrices: I defined weight matrices (W_h, W_i, W_w, W_m, W_P) to represent the relationships between the variables. These matrices captured the system’s behavior and were crucial for the parameter fitting process.
- Recurrent Neural Network: I represented the model as a recurrent neural network (RNN), where the input was the outdoor temperature, and the output was the heating power. The hidden nodes performed matrix multiplications of inputs and weights, without bias or activation functions. The output node used a ReLU (Rectified Linear Unit) activation function.
- Training and Testing: After training the model with historical data, I tested the resulting parameters against actual heating load data. This step ensured that the physical model’s output matched the real heating loads accurately.
Advantages of the Model
The physical-neural network model that I developed offers several significant advantages:
- Control Actions Modeling: Unlike traditional models, this approach accurately models the impact of control actions on heating systems. For instance, it can simulate how turning the heating off during high electricity prices affects the system’s behavior.
- Demand Response Optimization: By incorporating control actions into the model and accurately estimating parameters, the method can optimize demand response programs. Utility companies can use this to offer customized control strategies that smooth demand curves and reduce peak loads.
Conclusion
I am excited about the potential impact of my research. The combination of differential equations and neural networks in the physical-neural network model provides a powerful tool for estimating heating system parameters accurately. This approach offers precise control action modeling and opens the door to more effective demand response programs. Ultimately, it can lead to more efficient heating systems, energy savings, and improved comfort for users.
More details in the published research paper: https://ieeexplore.ieee.org/abstract/document/10267709
Feel free to reach out for full python code.